PICARD (ÉMILE)

PICARD (ÉMILE)

Le mathématicien français Charles Émile Picard fut un analyste profond et inspiré, un travailleur infatigable et un professeur captivant. Trois guerres le frappèrent durement, mais sa carrière ne compta que des succès rapides: agrégé et docteur la même année, à vingt et un ans; professeur à la Sorbonne à vingt-cinq ans, membre de l’Académie des sciences à trente-trois ans; secrétaire perpétuel de cette académie pendant près d’un quart de siècle, il connut encore, en 1924, l’honneur de représenter la science à l’Académie française.

L’œuvre de Picard n’est dépassée en importance que par celle de son génial contemporain Henri Poincaré: la liste de ses publications dans les périodiques scientifiques compte plus de trois cents titres; les résultats qu’il obtint lui-même et les recherches qu’il suscita sont également remarquables.

Les théorèmes de Picard en théorie des fonctions

Le plus célèbre théorème de Picard figure dans une note aux Comptes rendus de l’Académie des sciences (C.R.A.S. ), datée du 19 mai 1879, sous sa forme primitive, et dans les Annales de l’École normale supérieure de 1880 sous la forme suivante: Si z ⁰ est point singulier essentiel isolé de la fonction méromorphe f , celle-ci, dans un voisinage de z ⁰, ne peut omettre que deux valeurs au plus. La beauté du résultat, le meilleur possible comme le montre l’exemple simple f (z ) = th z , z ⁰ = 秊, est encore rehaussée par une démonstration savante et merveilleusement habile, où le but est atteint alors qu’il semble lointain.

Aucun théorème sans doute ne fut plus stimulant pour la théorie des fonctions: on chercha une démonstration plus directe; on remplaça les points où f prend une valeur donnée par ceux où f et une fonction algébrique donnée ont une valeur commune; on restreignit le voisinage de z ⁰ à un angle de sommet z ⁰; enfin on affina le théorème en ajoutant à l’alternative «f prend ou omet la valeur a » une évaluation de |f (z ) 漣 a |, ce qui mena le Finlandais Rolf Nevanlinna à remplacer la notion de valeur omise par celle, plus nuancée, de défaut.

D’après le théorème de Picard sur l’uniformisation, paru pour la première fois dans une note aux C.R.A.S. du 19 février 1883, si z ⁰ est point singulier essentiel isolé de deux fonctions méromorphes, celles-ci ne peuvent pas être liées par une relation algébrique de genre 礪 1; autrement dit, une relation algébrique de genre 礪 1 ne peut pas être uniformisée par des fonctions méromorphes à points singuliers isolés, alors qu’elle peut toujours l’être par des fonctions méromorphes plus générales, celles que Poincaré découvrit et appela fuchsiennes.

Équations fonctionnelles

Picard s’intéressa à maintes généralisations des fonctions elliptiques ou doublement périodiques. Dans ce domaine, son nom est attaché à l’équation fonctionnelle:

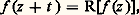où la fonction f est l’inconnue, tandis que le nombre t et la fonction rationnelle R sont donnés: dans une note aux C.R.A.S. du 9 octobre 1893, il montrait que cette équation, comme celle de Poincaré:

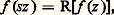si |s | 礪 1, a toujours des solutions méromorphes sur tout le plan.

D’autre part, Riemann avait affirmé, sans preuve suffisante, que: Si une fonction f méromorphe sur Cⁿ a 2 n périodes linéairement indépendantes sur R, ou bien ces périodes sont liées par certaines relations, ou bien f peut s’exprimer en fonction de moins de n variables. Dans une note aux C.R.A.S. du 3 décembre 1883, Picard et Poincaré démontrèrent ce théorème fondamental, puis, reprenant seul la question pour n = 2, Picard remarqua, dans une note du 18 mars 1889, que: Si l’on autorise f à avoir des singularités essentielles, alors les quatre périodes peuvent être choisies arbitrairement.

Les fonctions méromorphes quadruplement périodiques de deux variables, généralisant directement les fonctions elliptiques, permettent de représenter paramétriquement certaines surfaces algébriques, qui firent l’objet d’importants travaux sous le nom de surfaces hyperelliptiques.

Groupes discontinus

On sait que les substitutions modulaires:

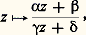où 見, 廓, 塚, 嗀 sont des entiers réels et où 見嗀 漣 廓塚 = 1, forment un groupe discontinu d’applications holomorphes du demi-plan:

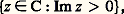sur lui-même. Dans le groupe de Picard , opérant sur le plan lui-même, les entiers 見, 廓, 塚, 嗀 sont complexes; pour rendre ce groupe discontinu, une note au Bulletin de la Société mathématique de France (S.M.F.), du 7 mars 1884, le prolonge, comme suit, du plan de la variable complexe z ou plan de base, au demi-espace qu’il limite, rapporté à z = 﨡 + i 兀 et à une cote 礪 0, autrement dit aux trois variables réelles 﨡, 兀, 﨣.

Comme une substitution S du groupe transforme une circonférence du plan de base en une autre, et deux circonférences orthogonales en deux autres circonférences orthogonales, elle transforme le réseau orthogonal à la circonférence imaginaire, section par le plan de base de la sphère-point ( 﨡, 兀, 﨣), en le réseau orthogonal à une autre circonférence imaginaire, section par le plan de base d’une autre sphère-point ( 﨡 , 兀 , 﨣 ); alors, la formule:

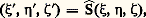définit le prolongement S de S au demi-espace.

Ce groupe de Picard est lié à la réduction modulaire des formes hermitiennes:

x et y étant des variables complexes, a et c des constantes réelles, b une constante complexe; si cette forme est définie, h (z , 1) = 0 est l’équation dans le plan de base d’une circonférence imaginaire, section d’une sphère-point ( 﨡, 兀, 﨣); ce point, dit représentatif de la forme h , n’est invariant que par un nombre fini de substitutions S puisque celles-ci forment un groupe discontinu; autrement dit, h n’est invariante que par un nombre fini de substitutions modulaires à coefficients complexes.

Si au contraire h est indéfinie, h (z , 1) = 0 est l’équation dans le plan de base d’une circonférence réelle: celle de rayon 1 ayant l’origine pour centre dans le cas le plus simple h (x , y ) = x 異 漣 y 北 ; cette circonférence peut être conservée par une infinité de substitutions S formant un groupe fuchsien. Dans un mémoire communiqué aux Acta mathematica de 1882, Picard renouvelle cette idée en prenant h hermitienne indéfinie à trois variables, et obtient les groupes hyperfuchsiens; de même que Poincaré construit des fonctions méromorphes d’une variable invariante par les substitutions d’un groupe fuchsien, automorphes pour ce groupe comme on dit aujourd’hui, deux d’entre elles étant liées algébriquement, de même Picard construit des fonctions méromorphes de deux variables automorphes pour un groupe hyperfuchsien, trois d’entre elles étant liées algébriquement.

On sait d’autre part que, parmi les fonctions automorphes pour des groupes fuchsiens particuliers, figure la fonction u (x ) obtenue par inversion de la relation:

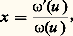où 諸 et 諸 sont deux fonctions de la forme:

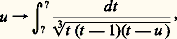et les ? pris parmi 0, 1, u , 秊. Exploitant cette idée dans son mémoire paru aux Acta mathematica de 1883, Picard aboutit à des fonctions automorphes u (x , y ), v (x , y ) pour certains groupes hyperfuchsiens par inversion des relations:

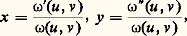où 諸, 諸 , 諸 sont trois fonctions de la forme:

les exposants 見, 廓,, 猪 étant convenablement choisis et les ? pris parmi 0, 1, u , v , 秊.

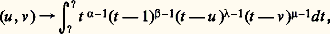Les fonctions algébriques et leurs intégrales

Picard aborda le domaine des fonctions algébriques et de leurs intégrales par une note aux C.R.A.S. , du 21 février 1881, sur les intégrales abéliennes :

où R est une fonction rationnelle donnée de deux variables et y (x ) une fonction algébrique donnée, autrement dit (x , y ) le point courant d’une courbe algébrique donnée, non unicursale. Une première généralisation, commencée par Max Nöther, concernait les intégrales doubles:

où R est une fonction rationnelle donnée de trois variables et (x , y , z ) le point courant d’une surface algébrique donnée, non unicursale.

Picard considère aussi, sur la même surface, les intégrales simples de différentielles totales, c’est-à-dire localement exactes, de la forme: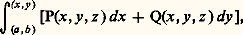

où P et Q sont des fonctions rationnelles données de trois variables. Il leur consacre un long mémoire qui reçut le grand prix des Sciences mathématiques pour 1888. Les problèmes qui se posent (combien d’intégrales linéairement indépendantes, avec des propriétés données, peut-on former sur une surface donnée?) soulèvent bien des difficultés, de topologie entre autres, qui ne furent pas toutes résolues par Picard, mais lui-même et ses contemporains y trouvèrent un champ de recherche vaste et fertile.

La méthode de Picard

On appelle souvent méthode de Picard la méthode des approximations successives, dont les applications sont nombreuses: aux équations aux dérivées partielles (dans le Journal de Liouville de 1890); aux équations différentielles (dans une note du 18 mars 1891 au Bulletin de la S.M.F.); aux équations intégrales (cf. équations INTÉGRALES, chap. 2). Tout cela se tient: ainsi, pour appliquer la méthode à l’équation différentielle du premier ordre y = f (x , y ), on remplace cette équation et la condition initiale y (a ) = b par l’équation intégrale:

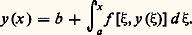La méthode s’applique aussi à la recherche de fonctions implicites, à la résolution d’équations fonctionnelles, à l’inversion d’un élément voisin de l’unité dans une algèbre de Banach unitaire. Dans chaque problème, une hypothèse appropriée est nécessaire pour que la suite des approximations converge; c’est pourquoi la méthode de Fredholm pour les équations intégrales (cf. équations INTÉGRALES, chap. 3), celle d’Arzela pour les équations différentielles ont un champ d’application plus vaste. Cependant, lorsque l’hypothèse appropriée est satisfaite, elle permet souvent de montrer l’unicité de la solution du problème en même temps que son existence.

Parmi les nombreuses recherches de Picard sur les équations aux dérivées par tielles, il faut encore signaler celles d’équations linéaires du second ordre, du type elliptique, dont les solutions ont les mêmes propriétés fondamentales que les fonctions harmoniques, solutions de l’équation de Laplace: analyticité, réponse unique au problème de Dirichlet, existence de solutions se comportant, au voisinage de l’origine, comme lg (x ² + y ²), dans le cas de deux variables x , y . Les développements de ces recherches conduisirent d’une part à la théorie moderne du potentiel, d’autre part à l’étude générale des équations linéaires dont toutes les solutions sont analytiques, ou indéfiniment différentiables (cf. équations aux DÉRIVÉES PARTIELLES, chap. 3).

Encyclopédie Universelle. 2012.